|
 |
 |
 |
 |
 |
 |
|
Signal Transport - Instrumentation Amplifiers
This section is about Op-Amps in an overall way. Ultimately we will look at practical analogue implementations using Op-Amps which solve the signal transport problem. Before we do, there is some prior information we need to delve into. This relates to the way in which we'll actually be signalling; the way in which the wires will be used. This is important because using wires for communication in electronics is still a common concept despite the digital world we now live in! So far I've shown some amplifier configurations that allow simple computations to be performed on electronic signals. Typically these signals are representations of real world quantities. Perhaps the voltage on a conductor represents the temperature of a block of metal. Alternatively a current in a wire might represent the fluid level in a barrel. Modern systems typically will encode analogue information like this as a digital word, so that a two's compliment adder or multiplier can perform numeric operations. Actually, although we're also looking at the implementation of analogue mathematical operators, it's usually preferable to do the maths at a better degree of precision, repeatability, and physical compactness in the digital world. The reason it's usually better to do maths digitally is mainly about the limitation of the electronic technology used to implement typical systems. Different signalling schemes impart different kinds of distortion onto the signals that they represent.
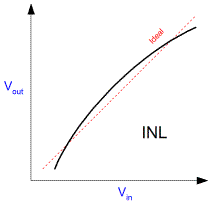
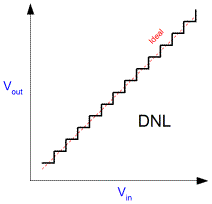
Although analogue amplifiers are usually designed to be linear, most of the time they are not. Normally in analogue systems differential (non)linearity (DNL) is good but integral (non)linearity (INL) is relatively poor. It's not really surprising since the transistors that the amplifiers are made from are basically logarithmic devices. Some of that logarithmic behaviour inevitably imaprts itself onto the signal. Digital systems are easily made linear in the gross sense. Just as ten one pound coins are exactly ten times greater than a single one, integral non-linearity (INL) is excellent in the digital system. The problem is that the scheme is synthetic and thus discontinuous. Differential non-linarity (DNL) can be poor, especially when the dynamic range is low in, say, an eight bit system. The price of carrots changes often, and unfortunately the price is usually somewhere between one and two pounds. If the scheme only has pounds for for the purpose of expressing price, it cannot express the price properly. There are ways in which analogue systems can be preferable for computation. Linearity, Size, Speed, Latency, continuity in time are all reasons. There are many ways in which a sensor system can be implemented. Their relative merits are not important here. A signal might be digitised before it is transmitted, or after. In either case it will be subject to noise in transit. Such noise couples into the signal by virtue of the signal travelling down a copper wire. It might be considered that the digital signal is invulnerable to such influences, but this isn't the case. It turns out that the same rules as everywhere else apply.
A low bandwidth digital signal is, more or less, invulnerable to noise. Obviously the basic analogue transmission capacity of a wire has a very wide bandwidth. It turns out that as the digital signal transmission bandwidth rises toward that of the underlying analogue capacity of the wire, the vulnerability of the signal to noise rises. The overriding rule that applies everywhere is that narrow band signals have much better inherent signal to noise ratio than wideband ones. Due to this phenomenon, it is possible for narrow band signals to have better dynamic range. In articles elsewhere on this site I'll be examining sampling, and digital ~ analogue conversion. Nowhere is the above phemomena clearer.Ultimately the phenomenon has it's roots in the Heisenberg uncertainty principle. It is a fundamental physical property of noise and measurement uncertainty. It's probably important to consider some of the pratical things that might drive decisions to adopt either analogue or digital signal transmission schemes. Up front must come the ubiquity of digital communications; everyone else does - so should we - right? Obviously these days the components, the materials from which a communications scheme is manufactured are readily available. It makes the digital decision easier. Other things, however, might influence the decision. Size, resilience, simplicity, cost.
Some very high temperature sensors might need signal senders which are very specialist. For high temperature one can, also read "high radiation hardness". It is simply inappropriate to put silicon based technologies into the beamline of an x-ray generator. Such technologies would immediately fail. A Cadmium Zinc Telluride (CZT) sensor to measure spatial variations in radiation flux relies on the bandgap just as with silicon. By contrast, CZT could take the punishment, and is capable of generating a signal which can be sent to a silicon based receiver which is suitably protected from the radiation flux by distance and shielding. The Strowger telephone switch is history, but still, most land based telephone lines are analogue. It's really hard for a digital multiplex to compete when the copper infrastructure is already present. That said, the advent of ADSL means that new requirements have come along and absorbed the redundant capacity. From a practical perspective there is still analogue communication occuring between the exchange and the consumer. Even in the modern world, sometimes especially in the advanced technology sector, analogue communications are critically important. In the round, the wiring of the line is the first concept to visit, even though it has no Op-Amps. In a sensor system the line might be connected directly to the actual sensor. The connected sensor undergoes whatever physical process to convert a real world quantity into an electrical analogue. Such a process might be something like the Thermoelectric effect, in a Thermocouple. A temperature difference directly creates an electrical potential or voltage at a junction between different metals. The wires of the line carry that signal voltage away. Alternatively, the same sensor could have been amplified and its output converted to some new signal. The circuit that would place such signals on the line could be built from Op-Amps, and would be described as a line driver. This then, is the second point of call. Finally, in any of the above cases, something is required to sit at the receiving end of the line and convert the signal from the sensor, or the line driver back into a usable signal for digitisation. Such a circuit could also be built from Op-Amps and is described as an instrumentaion amplifier. |
Copyright © Solid Fluid 2007-2025 |
Last modified: SolFlu Thu, 28 Mar 2013 18:32:12 GMT |